“One day a biologist walked into my office at the University of Michigan and asked if I could help him with a combinatiorial problem. He wanted to investigate a theory of evolution for very small animals, beginning with one cell and growing just one cell at a time.” -- Frank Harary, “Achieving the Skinny Animal," Eureka, Summer 1982

Meet the "animals" - these quirky geometric patterns are the heart of the game, named by mathematician Frank Harary who mapped out this fascinating variant in the late 1970s. The game has been called Harary's tic-tac-toe or animal tic-tac-toe.

🎯 Target Animals

The set of possible target animals to choose from, one of which will be the target in a given game, are as follows:

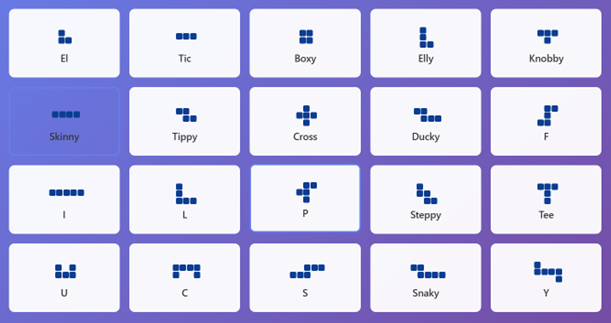
Click on any pattern to select it as your target for the game. Each pattern has unique strategic properties and varying numbers of possible orientations.

🎲 Game Board

The board is a square grid of tiles, with size selectable from 3x3 to 10x10. For example, a 7x7 grid:

The game board consists of clickable squares where players place their pieces. Board sizes range from 3x3 to 10x10, with larger boards offering more strategic possibilities.

🎮 Gameplay

You can play against another human, challenge an AI, or watch AI players battle it out! Players take turns until one of them creates the target animal.

For example, in this case the human player (shamrock tiles) was able to successfully place the given target animal Tippy and win the game!

The game shows a completed board with the winning pattern formed by the player's pieces. The target animal "Tippy" has been successfully placed, resulting in a victory!

Pattern Orientations

For Tippy, there are 4 such orientations:

The Tippy pattern can be rotated and reflected to create 4 unique orientations. Any of these orientations counts as a valid win condition.

For some, like Elly, there are 8:

The Elly pattern has 8 unique orientations due to its L-shape, allowing for more flexibility in placement compared to patterns like Tippy.

Others, like Cross and Boxy, may have just one unique orientation:

Some patterns like Cross and Boxy have only one unique orientation, making them more predictable but potentially easier to block.

🤖 Meet Your AI Opponents

Each AI player has a unique personality and playing style. Will you challenge the methodical Frank Harary, the aggressive Paul Erdős, or the unpredictable Squirrel?

The default players are Human (you) and Computer (Frank Harary). In all there are nine computer players to select from:

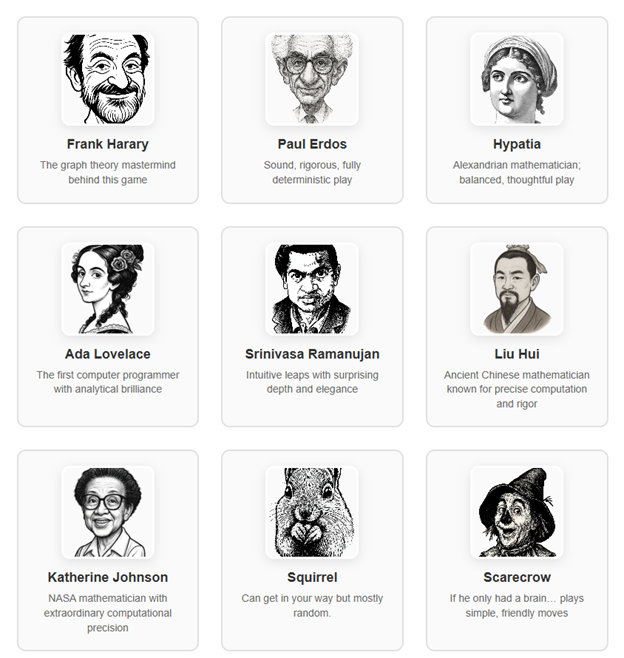
Each AI player has a unique personality and playing style, from the methodical Frank Harary to the unpredictable Squirrel. Choose your opponent based on your preferred challenge level!

🎛️ Game Controls

Player Setup

Player 1 goes first, so in Human vs. Computer games, it's best for flexibility to have Human as Player 1 and Computer as Player 2. If you (the Human) want to let the Computer play first, that can be accomplished by clicking on PASS.

Timeline Navigation

The arrow controls are back and step, for possibly going back and forth in the current timeline. This allows you to recapitulate the game if desired. If at any prior point in the timeline you select a different square than the one you had previously chosen in the current timeline, a "new timeline" message is generated and the game proceeds from that new branch. This allows you to take back moves.

Computer vs. Computer Mode

In computer vs. computer mode, game play between the players is automatic and the controls are a little different:

• Play Button - Start or resume automatic gameplay
• Pause Button - Pause the automatic gameplay
• Back/Step - Move through the timeline when paused

🎲 Game Characteristics

🧠 Strategy

Core Strategic Principles

1. Pattern Recognition

• Study the target pattern carefully before making your first move
• Identify all possible orientations and positions where the pattern can be completed
• Look for "hot spots" - squares that are part of multiple potential winning configurations

2. Offensive Strategy

• Create Multiple Threats: Try to place pieces that contribute to multiple potential winning patterns simultaneously
• Center Control: Many patterns benefit from controlling central squares, especially on larger boards
• Pattern-Specific Approaches:
  • Line patterns (Skinny): Control the center and work toward edges
  • Square patterns (Fatty, Boxy): Create multiple square threats in different areas
  • T-shaped patterns (Tippy, Knobby): Use the center and build outward
  • L-shaped patterns (Elly): Control corners and build the pattern systematically

3. Defensive Strategy

• Block Critical Squares: When your opponent is close to winning, identify and block the most threatening squares
• Fork Prevention: Look ahead to prevent your opponent from creating multiple winning threats
• Pattern Awareness: Understand which patterns are most likely to be completed given the current board state

4. Board Size Considerations

• Small boards (3x3, 4x4): Games are often quick and decisive; focus on immediate threats
• Medium boards (5x5, 6x6): Balance between offense and defense; look for strategic positioning
• Large boards (7x7+): More complex strategy; control key areas and create multiple threats

Advanced Tactics

The Two-Move Threat

Create a position where you can win in two different ways on your next turn. This forces your opponent to block one threat, allowing you to complete the other.

Pattern Interference

Use your pieces to interfere with your opponent's pattern while advancing your own. A well-placed piece can serve both offensive and defensive purposes.

Timing and Tempo

• Early Game: Focus on controlling key squares and creating multiple threats
• Mid Game: Balance between advancing your pattern and blocking your opponent
• End Game: Look for forced wins or defensive moves that prevent immediate loss

Pattern-Specific Strategies

El

For the player with the opening move, El is unstoppable on any board 3x3 or larger:

• Select a central square.
• Select another central square to make 2-in-a-row,
• Complete El.

---

Tic

On a 4x4 or larger board, the player with the opening move can force a Tic win in three moves:

• 1. Select a central square.
• 2. Select another available central square that gives you 2-in-a-row with open ends.
• 3. Complete Tic.

---

Elly

On a 4x4 or larger board, the player with the opening move can force an Elly win in four moves:

• Follow the Tic strategy above to make 3-in-a-row.
• Complete Elly (at least one winning move will be available).

---

Knobby

On a 5x5 or larger board, Knobby can also force a win in four moves:

• 1. Select a central square as the opening move.
• 2. Select a square diagonal from the opening move that is not adjacent to the opponent's piece.
• 3. Select a square adjacent to your first two pieces (forming El) that is not adjacent to either of the opponent's pieces. This creates a fork.
• 4. Complete Knobby.

---

Tippy

Tippy is a forced win in four moves very much along the lines above for Knobby:

• Achieve El as with the Knobby strategy on move 3. This creates a Tippy fork.
• Complete Tippy.

---

Other known winners: Skinny, Ducky, L and Z

These four target patterns are known to be forced wins with optimal play on sufficiently large boards, but the strategies can be complex and are left as exercises for the player!

---

Snaky

Snaky is unique among the polyanimals--it's unknown with mathematical certainty whether Snaky is a winner or loser and under what conditions (e.g. minimum board size). Harary (1982) conjectured that Snaky is a winner on a large enough board:

"My plausibility consideration for this assertion is that my former student, Dr. Geoffrey Exoo, won his last 20 games of Snaky achievement played on a sheet of graph paper."

If Harary's conjecture is true, then Snaky is the only winner among the hexominoes. There are no forced winners among heptominoes or greater.

Of course, this all is predicated on perfect, optimal play. With imperfect play on the part of the opponent, any pattern can be a winner!

---

Psychological Elements

Against AI Players

• Strong AI (Erdős, Harary, Johnson): Play defensively and look for AI mistakes in complex positions
• Weaker AI (Scarecrow, Squirrel): Be more aggressive; they may miss defensive moves
• Mixed AI (Hypatia): Adapt your strategy based on the specific AI's playing style

Against Human Players

• Bluffing: Sometimes make moves that appear threatening but aren't immediately winning
• Pattern Confusion: Use pieces that could be part of multiple patterns to confuse your opponent
• Tempo Control: Vary your playing speed to unsettle your opponent

Practice and Improvement

1. Study Pattern Transformations: Understand how each pattern can be rotated and reflected
2. Analyze Completed Games: Review your games to identify missed opportunities
3. Practice Against Different AI Levels: Start with weaker AI and work your way up
4. Experiment with Different Board Sizes: Each size offers different strategic challenges
5. Watch AI vs AI: Observe different AI players compete to learn new strategies

Common Mistakes to Avoid

• Tunnel Vision: Focusing only on your own pattern while ignoring your opponent's threats
• Over-Committing: Placing too many pieces in one area without considering the opponent's responses
• Ignoring the Center: Many patterns benefit from central control, especially on larger boards
• Poor Timing: Making defensive moves too early or offensive moves too late